What is Asymptotic Notations and how to design and analysis of algorithms with examples

There are many solutions for a particular problem.Means, For one problem we can design more than one algorithms.But how to find which algorithms are good and which are bad.

There are two ways to find the Ideal Algorithms for any particular problem as given  below:-

1. Time:-An algorithm is good which takes less time.
2. Space:-An algorithm is good which takes less space(storage).

The efficiency of any algorithms fully dependent on time,space and other resources which are needed to execute any algorithms. 

Asymptotic Notations:-

Asymptotic notations are the mathematical notations.It is used to represent the complexity of algorithms.This allows us to analyze an algorithm's running time and its behaviors. There are mainly three asymptotic notations to find the complexity of algorithms as given below:-

1. Big O Notation
2. Big Ω (omega) Notation
3. Big Θ (theta) Notation

1.) Big O Notation:-

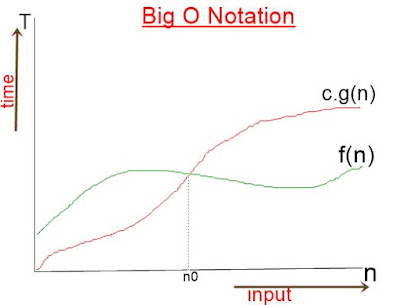
Big O notation always represents the upper bound of running time of any algorithms. To represent the worst case complexity we always use Big O notation.Big o notation always talk about worst case complexity of an algorithm.

Y Axis Represents--> Time

X Axis Represents--> Input data

Mathematical formula:-

f(n)<=c.g(n)

n>=n0

c>0,n0>=1

f(n)=O(g(n))

f(n)=Big O of g(n)

Descriptions:-

• f(n) always less than or eual to c.g(n).
• c,n is a constant that is always greater than zero.
• n0 is greater than or equal to 1.

Note:-If we are talking about Big O notation,two pictures comes in our mind.

1. Upper Bound
2. Worst case

e.g.

# Find the 50 element in given array using Linear search .

When we start search 50 element in array, we find this element at the last index of the array.This is a worst case for searching this element.When we find the element at zero index of array then it is called best case for that particular element.Big o Notation represents the worst case complexity.

Time complexity =O(9)

2.) Big Ω (omega Notation:-

Big Ω notation always represents the lower bound of running time of any algorithms.To represent the best case complexity we always use Big Ω notation.Big Ω notation always talk about best case complexity of an algorithm.

Y Axis Represents--> Time

X Axis Represents--> Input data

Mathematical formula:-

f(n)>=c.g(n)

n>=n0

c>0,n0>=1

f(n)=Ω(g(n))

f(n)=Big Ω of g(n)

Descriptions:-

• f(n) always greater than or eual to c.g(n).
• c,n is a constant that is always greater than zero.
• n0 is greater than or equal to 1.

Note:-If we are talking about Big Ω notation,two pictures comes in our mind.

1. Lower Bound
2. best case

e.g.

# Find the 15 element in given array using Linear search .

When we start search 15 element in array, we find this element at the first index of the array.This is a best case for searching this element.Big Ω Notation represents the best case complexity.

Time complexity =Ω(0)

3.) Big Θ (theta) Notation:-

Big Θ notation represents the average case time complexity of an algorithm.

Y Axis Represents--> Time

X Axis Represents--> Input data

Mathematical formula:-

c1.g(n)<=f(n)<=c2.g(n)

n>=n0

c1,c2>0

n0>=1

f(n)=Θ(n)

f(n)=Big Θ of g(n)

Note:-If we are talking about Big Θ notation,one pictures comes in our mind.

• Average value (present in middle part)

e.g.

# Find the average marks of 12 students out of 100 marks.

In above table ,Average Marks of 12 students =53.33 which presents between 1 to 100. Big Θ Notation is used to represents the average case.so time complexity of this will represent by Big  Θ Notation.

f(n)>=1 & f(n)<=100

1<=f(n)<=100

Time complexity =Θ(53.33)

Watch Complete Lecture Video:-

For More...

1. How to access elements in string with examples
2. String operators in python with examples
3. String properties in python with examples
4. Search and Replace functions in python
5. call by value and call by reference in c#
6. Ajax concepts in .net